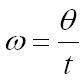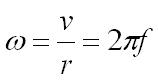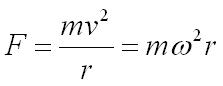Linear motion
Linear motion, also called uniform motion or rectilinear motion, motion in one spatial dimension. According to Newton’s first law (also known as the principle of inertia), a body with no net force acting on it will either remain at rest or continue to move with uniform speed in a straight line, according to its initial condition of motion. In fact, in classical Newtonian mechanics, there is no important distinction between rest and uniform motion in a straight line; they may be regarded as the same state of motion seen by different observers, one moving at the same velocity as the particle, the other moving at constant velocity with respect to the particle. A body in motion may be said to have momentum equal to the product of its mass and its velocity. It also has a kind of energy that is entirely due to its motion, called kinetic energy. The kinetic energy of a body of mass m in motion with velocity v is given by K = (1/2)mv2.
Speed and Velocity
Both speed and velocity tell us how far something is travelling in unit time. As velocity is a vector it must also tell us what direction the object is travelling in.
Average velocity v̅ = Δs / Δt
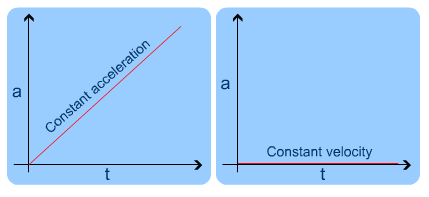
Acceleration
Acceleration tells us how rapidly something is changing velocity – for instance, the change in velocity in unit time.Deceleration is the same thing, but has a negative sign as the velocity if decreasing.
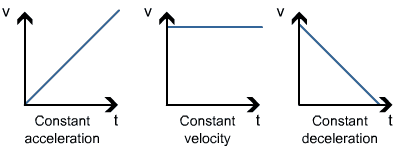
Velocity-time graphs
These are similar to displacement-time graphs, but this time velocity is on the y-axis. Here are the only possibilities that you’ll come across at A-level.
gradient = change in V (or ΔV) / change in t (or Δt) = the acceleration at any time.
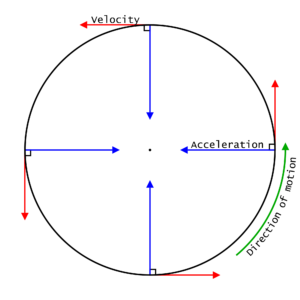
Circular motion
When an object moves in a circle at a constant speed its velocity (which is a vector) is constantly changing. Its velocity is changing not because the magnitude of the velocity is changing but because its direction is. This constantly changing velocity means that the object is accelerating (centripetal acceleration). For this acceleration to happen there must be a resultant force, this force is called the centripetal force.
Angular Speed
The angular speed (w) of an object is the angle (q) it moves through measured in radians (rad) divided by the time (t) taken to move through that angle. This means that the unit for angular speed is the radian per second (rad s-1).
v is the linear velocity measured in metres per second (ms-1).
r is the radius of the circle in metres (m).
f is the frequency of the rotation in hertz (Hz).
Centripetal Acceleration
Centripetal acceleration (a) is measure in metres per second per second (ms-2). It is always directed towards the center of the circle.
Centripetal Force
When an object moves in a circle the centripetal force (F) always acts towards the centre of the circle. The centripetal force, measured in newtons (N) can be different forces in different settings it can be gravity, friction, tension, lift, electrostatic attraction etc.
Vibrationational motion
periodic back-and-forth motion of the particles of an elastic body or medium, commonly resulting when almost any physical system is displaced from its equilibrium condition and allowed to respond to the forces that tend to restore equilibrium.
Vibrations fall into two categories: free and forced. Free vibrations occur when the system is disturbed momentarily and then allowed to move without restraint. A classic example is provided by a weight suspended from a spring. In equilibrium, the system has minimum energy and the weight is at rest. If the weight is pulled down and released, the system will respond by vibrating vertically.
The vibrations of a spring are of a particularly simple kind known as simple harmonic motion (SHM). This occurs whenever the disturbance to the system is countered by a restoring force that is exactly proportional to the degree of disturbance. In this case, the restoring force is the tension or compression in the spring, which (according to Hooke’s law) is proportional to the displacement of the spring. In simple harmonic motion, the periodic oscillations are of the mathematical form called sinusoidal.
Most systems that suffer small disturbances counter them by exerting some form of restoring force. It is frequently a good approximation to suppose that the force is proportional to the disturbance, so that SHM is, in the limiting case of small disturbances, a generic feature of vibrating systems. One characteristic of SHM is that the period of the vibration is independent of its amplitude. Such systems therefore are used in regulating clocks. The oscillation of a pendulum, for instance, approximates SHM if the amplitude is small.
A universal feature of free vibration is damping. All systems are subject to frictional forces, and these steadily sap the energy of the vibrations, causing the amplitude to diminish, usually exponentially. The motion is therefore never precisely sinusoidal. Thus, a swinging pendulum, left undriven, will eventually return to rest at the equilibrium (minimum-energy) position.
Forced vibrations occur if a system is continuously driven by an external agency. A simple example is a child’s swing that is pushed on each downswing. Of special interest are systems undergoing SHM and driven by sinusoidal forcing. This leads to the important phenomenon of resonance. Resonance occurs when the driving frequency approaches the natural frequency of free vibrations. The result is a rapid take-up of energy by the vibrating system, with an attendant Growth of the vibration amplitude. Ultimately, the growth in amplitude is limited by the presence of damping, but the response can, in practice, be very great. It is said that soldiers marching across a bridge can set up resonant vibrations sufficient to destroy the structure. Similar folklore exists about opera singers shattering wine glasses.
Electric vibrations play an important role in electronics. A circuit containing both inductance and capacitance can support the electrical equivalent of SHM involving sinusoidal current flow. Resonance occurs if the circuit is driven by alternating current that is matched in frequency to that of the free oscillations of the circuit. This is the principle behind tuning. For example, a radio receiver contains a circuit, the natural frequency of which can be varied. When the frequency matches that of the radio transmitter, resonance occurs and a large alternating current of that frequency develops in the circuit. In this way, resonating circuits can be used to filter out one frequency from a mixture.
In Musical instruments, the motion of strings, membranes, and air columns consists of a superposition of SHM’s; in engineering structures, vibrations are a common, though usually undesirable, feature. In many cases, complicated periodic motions can be understood as the superposition of SHM at many different frequencies.
,
Linear Motion
Linear motion is the motion of an object along a straight line. It is the simplest type of motion to analyze, and it is the basis for all other types of motion.
There are two types of linear motion: rectilinear motion and uniform motion.
Rectilinear motion is motion in a straight line. It can be either uniform or non-uniform.
Uniform motion is motion in a straight line at a constant speed. The speed of an object is the distance it travels per unit of time.
Non-uniform motion is motion in a straight line at a variable speed. The acceleration of an object is the rate at which its speed changes.
Circular Motion
Circular motion is the motion of an object around a circle. It is a more complex type of motion than linear motion, and it requires the use of centripetal force to keep the object moving in a circle.
Centripetal force is the force that acts towards the center of a circle and keeps an object moving in a circular path. It is always perpendicular to the velocity of the object.
Centrifugal force is an apparent force that acts away from the center of a circle. It is not a real force, but it is a useful concept for understanding circular motion.
Vibrational Motion
Vibrational motion is the motion of an object that repeats itself over and over again. It is a type of oscillatory motion.
Simple harmonic motion is a special type of vibrational motion in which the restoring force is proportional to the displacement from equilibrium.
Periodic motion is any motion that repeats itself over and over again at regular intervals. The period of a motion is the time it takes to complete one cycle.
Amplitude is the maximum displacement of an object from its equilibrium position.
Frequency is the number of cycles per unit of time. The frequency of a motion is the reciprocal of the period.
Wavelength is the distance between two successive crests or troughs of a wave.
Phase is the position of a wave relative to a reference point.
Velocity is the rate of change of displacement. The velocity of a vibrating object is the rate at which its displacement changes.
Acceleration is the rate of change of velocity. The acceleration of a vibrating object is the rate at which its velocity changes.
Conclusion
In conclusion, linear motion, circular motion, and vibrational motion are all important types of motion. They are the basis for all other types of motion, and they are essential for understanding the physical world.
1. What is wave motion?
Wave motion is the transfer of energy through a medium from one point to another without the actual movement of the particles of the medium.
2. What are the different types of waves?
There are two main types of waves: mechanical waves and Electromagnetic Waves. Mechanical waves require a medium to travel through, while electromagnetic waves can travel through the vacuum of space.
3. What are the properties of waves?
The properties of waves include amplitude, wavelength, frequency, and speed. Amplitude is the height of the wave, wavelength is the distance between two consecutive crests or troughs, frequency is the number of waves that pass a given point in a given amount of time, and speed is the distance that a wave travels in a given amount of time.
4. What is the equation for wave motion?
The equation for wave motion is $y = A \sin(kx – \omega t)$, where $y$ is the displacement of the particle from its equilibrium position, $A$ is the amplitude of the wave, $k$ is the wave number, $\omega$ is the angular frequency, and $t$ is time.
5. What is the difference between transverse waves and longitudinal waves?
Transverse waves are waves in which the particles of the medium move perpendicular to the direction of the wave. Longitudinal waves are waves in which the particles of the medium move parallel to the direction of the wave.
6. What is the difference between a crest and a trough?
A crest is the highest point of a wave, while a trough is the lowest point of a wave.
7. What is the difference between a node and an antinode?
A node is a point on a standing wave where the displacement of the particles is zero, while an antinode is a point on a standing wave where the displacement of the particles is maximum.
8. What is the difference between constructive interference and destructive interference?
Constructive interference occurs when two waves of the same frequency and amplitude meet in phase, resulting in a wave with a larger amplitude. Destructive interference occurs when two waves of the same frequency and amplitude meet out of phase, resulting in a wave with a smaller amplitude.
9. What is the principle of superposition?
The principle of superposition states that the total displacement of a particle at a given point is equal to the sum of the displacements of the individual waves at that point.
10. What is the Doppler effect?
The Doppler effect is the change in the frequency of a wave as the source of the wave or the observer moves relative to each other.
11. What is the difference between red shift and blue shift?
Red shift is a decrease in the frequency of a wave, while blue shift is an increase in the frequency of a wave.
12. What is the application of wave motion?
Wave motion has many applications in science and technology, including Sound, Light, and radio waves.
A car is moving at a constant speed of 50 km/h. What is the car’s acceleration?
(A) 0 m/s^2
(B) 50 m/s^2
(C) 100 m/s^2
(D) 150 m/s^2A ball is thrown straight up into the air. What is the ball’s acceleration at the top of its flight?
(A) 0 m/s^2
(B) 9.8 m/s^2
(C) 19.6 m/s^2
(D) 29.4 m/s^2A roller coaster car is moving at a constant speed of 20 m/s around a circular track. What is the car’s centripetal acceleration?
(A) 0 m/s^2
(B) 4.4 m/s^2
(C) 9.8 m/s^2
(D) 19.6 m/s^2A pendulum swings back and forth. What type of motion is this?
(A) Linear motion
(B) Circular motion
(C) Vibrational motion
(D) Rotational motionA wave travels through a medium. What type of motion is this?
(A) Linear motion
(B) Circular motion
(C) Vibrational motion
(D) Wave motionA car is accelerating at a rate of 5 m/s^2. What is the car’s speed after 2 seconds?
(A) 10 m/s
(B) 15 m/s
(C) 20 m/s
(D) 25 m/sA ball is thrown straight up into the air. What is the ball’s velocity at the top of its flight?
(A) 0 m/s
(B) 9.8 m/s
(C) 19.6 m/s
(D) 29.4 m/sA roller coaster car is moving at a constant speed of 20 m/s around a circular track. What is the car’s centripetal force?
(A) 0 N
(B) 440 N
(C) 980 N
(D) 1960 NA pendulum swings back and forth. What is the period of the pendulum?
(A) The time it takes for the pendulum to swing from one side to the other and back again.
(B) The distance the pendulum swings from its equilibrium position.
(C) The speed of the pendulum.
(D) The acceleration of the pendulum.A wave travels through a medium. What is the wavelength of the wave?
(A) The distance between two consecutive crests of the wave.
(B) The distance between two consecutive troughs of the wave.
(C) The distance between a crest and a trough of the wave.
(D) The time it takes for one wave to pass a given point.