<<–2/”>a href=”https://exam.pscnotes.com/5653-2/”>p>sectors and segments of a circle, presented in the format you requested:
Introduction
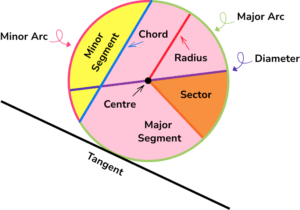
In the realm of geometry, a circleâa simple yet profound shapeâoffers fascinating divisions. Two of the most fundamental divisions are sectors and segments. While both are parts of a circle, they are distinct in their construction and properties.
Key Differences: Sector vs. Segment
| Feature | Sector | Segment |
|---|---|---|
| Definition | A part of a circle enclosed by two radii and their intercepted arc. | A region of a circle bounded by a chord and its corresponding arc. |
| Construction | Formed by cutting a “Pie slice” from the center of the circle. | Formed by cutting a piece away with a straight line (chord). |
| Contains | The circle’s center. | Does not contain the circle’s center (unless the chord is a diameter). |
| Shape | Always a portion of a circular disk. | Can be crescent-shaped or resemble a smaller portion of a disk. |
| Area Calculation | Involves the central angle and the radius. | Involves the central angle, radius, and trigonometry. |
Visual Representation
Advantages and Disadvantages
| Sector | Segment | |
|---|---|---|
| Advantages | Easier to visualize and calculate the area. Important for understanding angles and arc lengths. | More flexible in shape. Used in various geometric applications. |
| Disadvantages | Less flexible in shape. Limited by the angle and radius. | Area calculation can be more complex. Not directly related to central angles. |
Similarities
- Both are parts of a circle.
- Both are defined by arcs.
- Both have measurable areas.
FAQs
What is the difference between a major and minor sector?
A major sector has a central angle greater than 180 degrees, while a minor sector has a central angle less than 180 degrees.Can a segment be a sector?
Yes, a segment becomes a sector if the chord defining the segment is a diameter of the circle.What are some real-life applications of sectors and segments?
Sectors: Calculating the area of a pizza slice, understanding clock angles, designing pie charts.
Segments: Engineering (calculating cross-sectional areas), architecture (designing arches), measuring portions of land or bodies of water.How do I find the perimeter of a sector or segment?
Sector: Add the lengths of the two radii and the arc length.
Segment: Add the length of the chord and the arc length.Are there other ways to divide a circle?
Yes! Circles can be divided into annuli (ring-shaped regions), concentric circles (circles with the same center but different radii), and other shapes using combinations of chords, arcs, and radii.
Let me know if you’d like a deeper dive into any of these topics or have any other questions!