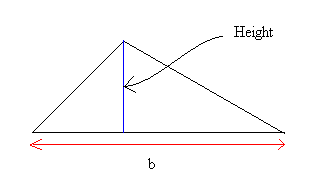
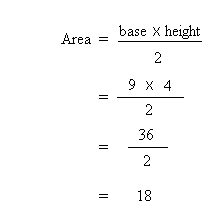The area of triangles can be found by using the following formula:
Area = Base × height / 2
The red line represents the length of the base (call it b if you want) and the blue line represents the length of the height.
To get the area, just multiply the value of the base by the value of the height and divide the result by 2.
Example:
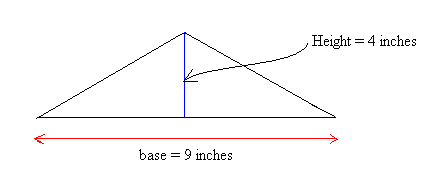
Find the area for the following figure:
The area is 18 square inches or 18 inches2.
Condition of collinearity of three points
Collinear points: Three points A, B and C are said to be collinear if they lie on the same straight line.
There points A, B and C will be collinear if AB + BC = AC as is clear from the adjoining figure.
In general, three points A, B and C are collinear if the sum of the lengths of any two line segments among AB, BC and CA is equal to the length of the remaining line segment, that is,
either AB + BC = AC or AC +CB = AB or BA + AC = BC.
In other words,
There points A, B and C are collinear if:
- AB + BC = AC i.e., Or,
- (ii) AB + AC = BC i.e. ,
- Or, AC + BC = AB i.e.,
Measure of angles
In the sexagesimal
In Sexagesimal System, an angle is measured in degrees, minutes and seconds.
A complete rotation describes 360°. In this system, a right angle is divided into 90 equal parts and each such part is called a Degree (1°); a degree is divided into 60 equal parts and each such part is called a Sexagesimal Minute (1’) and a minute is further sub-divided into 60 equal parts, each of which is called a Sexagesimal Second (1’’). In short,
1 right angle = 90 degrees (or 90°)
1 degree (or 1°) = 60 minutes ( or 60’)
1 minute ( or 1’ ) = = 60 seconds ( or 60’’)
In Centesimal System
In Centesimal System, an angle is measured in grades, minutes and seconds. In this system, a right angle is divided into 100.
equal parts and each such part is called a Grade (1g); again, a grade is divided into 100 equal parts and each such part is called a Centesimal Minute (1‵) ; and a minute is further sub-divided into 100 equal parts, each of which is called a Centesimal Second (1‶). In short,
1 right angle = 100 grades (or, 100g)
1 grade ( or 1g) = = 100 minutes (or, 100‵)
and 1 minute (or 1‵) = = 100 seconds ( or, 100‶).
Circular System
In this System, an angle is measured in radians. In higher mathematics angles are usually measured in circular system. In this system a radian is considered as the unit for the measurement of angles.
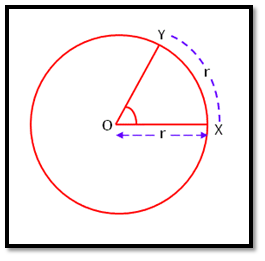
Radian: A radian is an angle subtended at the center of a circle by an arc whose length is equal to the radius.
In any circle, the angle subtended at its centre by an arc of the circle whose length is equal to the radius of the circle is called a radian. Let OX = r be the radius of a circle having center at O
Now, take an arc XY of the circle such that arc XY = r and join OY. By definition, ∠XOY = one radian. One radian is written as 1c, 2 radians as 2c and in general, k radians as kc.
Circular (radian) measure of an angle:
The circular measure of an angle is the number of radians it contains. Thus the circular (radian) measure of a right angle is π/2.
,
Area of a Triangle
The area of a triangle is the amount of space enclosed by its three sides. It can be calculated using the following formula:
$A = \frac{1}{2}bh$
where $b$ is the base of the triangle and $h$ is the height of the triangle.
The base of a triangle is the side opposite the right angle. The height of a triangle is the perpendicular distance from the base to the opposite vertex.
For example, if the base of a triangle is 5 cm and the height is 4 cm, then the area of the triangle is:
$A = \frac{1}{2}bh = \frac{1}{2} \times 5 \times 4 = 10$ cm$^2$
Condition of Co-linearity of Three Points
Three points are said to be collinear if they lie on the same line. The condition for three points to be collinear is that the sum of the two shorter sides must be greater than the longest side.
For example, the points $(1, 2)$, $(3, 4)$, and $(5, 6)$ are collinear because $3 + 4 > 5$.
Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It is used in many fields, including engineering, architecture, and navigation.
The three main trigonometric functions are sine, cosine, and tangent. The sine of an angle is the ratio of the opposite side to the hypotenuse. The cosine of an angle is the ratio of the adjacent side to the hypotenuse. The tangent of an angle is the ratio of the opposite side to the adjacent side.
The trigonometric functions can be used to solve triangles. For example, if you know the length of the hypotenuse and the sine of an angle, you can calculate the length of the opposite side.
Trigonometry can also be used to solve problems involving circles. For example, if you know the radius of a circle and the angle subtended by an arc, you can calculate the length of the arc.
Measure of Angles in the Sexagesimal System
The sexagesimal system is a system of measurement that uses 60 as its base. It is the most common system of measurement for angles.
In the sexagesimal system, an angle is measured in degrees. A degree is divided into 60 minutes, and a minute is divided into 60 seconds.
To measure an angle, you use a protractor. A protractor is a tool that has a scale of degrees around the edge. To measure an angle, you place the protractor on the line that represents the angle, and then line up the zero degree mark with one of the endpoints of the angle. The number of degrees that the protractor reads is the measure of the angle.
For example, if you place the protractor on the line that represents the angle, and then line up the zero degree mark with the endpoint of the angle that is on the left, the protractor will read 30 degrees.
Measure of Angles in the Contesimal System
The contesimal system is a system of measurement that uses 100 as its base. It is a relatively new system of measurement, and it is not as widely used as the sexagesimal system.
In the contesimal system, an angle is measured in centsimals. A centimal is divided into 100 millicentsimals, and a millicentimal is divided into 100 microcentsimals.
To measure an angle, you use a contesimal protractor. A contesimal protractor is a tool that has a scale of centsimals around the edge. To measure an angle, you place the protractor on the line that represents the angle, and then line up the zero centsimal mark with one of the endpoints of the angle. The number of centsimals that the protractor reads is the measure of the angle.
For example, if you place the protractor on the line that represents the angle, and then line up the zero centsimal mark with the endpoint of the angle that is on the left, the protractor will read 30 centsimals.
Measure of Angles in the Circular System
The circular system is a system of measurement that uses the circle as its base. It is a relatively new system of measurement, and it is not as widely used as the sexagesimal system or the contesimal system.
In the circular system, an angle is measured in radians. A radian is the angle subtended by an arc of a circle that is equal
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It is used in many fields, including engineering, surveying, and navigation.
What are the three main trigonometric functions?
The three main trigonometric functions are sine, cosine, and tangent. They are defined as follows:
- Sine is the ratio of the opposite side of a right triangle to the hypotenuse.
- Cosine is the ratio of the adjacent side of a right triangle to the hypotenuse.
- Tangent is the ratio of the opposite side of a right triangle to the adjacent side.
What is the Pythagorean theorem?
The Pythagorean theorem is a mathematical formula that relates the lengths of the sides of a right triangle. It states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.
What is the law of cosines?
The law of cosines is a mathematical formula that relates the lengths of the sides and angles of a triangle. It states that the square of any side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of those sides times the cosine of the angle between them.
What is the law of sines?
The law of sines is a mathematical formula that relates the lengths of the sides and angles of a triangle. It states that the ratio of the sine of any angle of a triangle to the length of the side opposite that angle is equal to the ratio of the sine of any other angle of the triangle to the length of the side opposite that angle.
What is the unit circle?
The unit circle is a circle with radius 1 centered at the origin of the coordinate plane. It is used to define the trigonometric functions.
What are the trigonometric identities?
The trigonometric identities are equations that are true for all values of the trigonometric functions. They are used to simplify trigonometric expressions and solve trigonometric equations.
What are the trigonometric graphs?
The trigonometric graphs are the graphs of the trigonometric functions. They are used to visualize the trigonometric functions and to understand their properties.
What are the applications of trigonometry?
Trigonometry is used in many fields, including engineering, surveying, and navigation. It is also used in physics, chemistry, and astronomy.
What are the history of trigonometry?
Trigonometry has a long and rich history. It was first developed by the ancient Greeks to solve problems in geometry and astronomy. It was later used by the Arabs and Europeans to develop navigation and surveying techniques. In the 17th century, trigonometry was used by Isaac Newton to develop calculus.
What are the future of trigonometry?
Trigonometry is a well-established field of mathematics with a long history. It is used in many fields and is likely to continue to be used in the future.
Sure, here are some MCQs on the topics of area of triangle, condition of co-linearity of three points, and trigonometry:
- The area of a triangle is equal to one half the product of its base and height. True or False?
- If three points are collinear, then they must lie on the same line. True or False?
- The sine of an angle is equal to the opposite side over the hypotenuse. True or False?
- The cosine of an angle is equal to the adjacent side over the hypotenuse. True or False?
- The tangent of an angle is equal to the opposite side over the adjacent side. True or False?
Answers:
1. True
2. True
3. True
4. True
5. True
Here are some additional MCQs on the topic of trigonometry:
- The trigonometric functions are defined for all real numbers. True or False?
- The trigonometric functions are periodic with period $2\pi$. True or False?
- The trigonometric functions are even functions. True or False?
- The trigonometric functions are odd functions. True or False?
- The trigonometric functions are increasing on the interval $(0,\pi/2)$. True or False?
Answers:
6. False
7. True
8. False
9. True
10. False