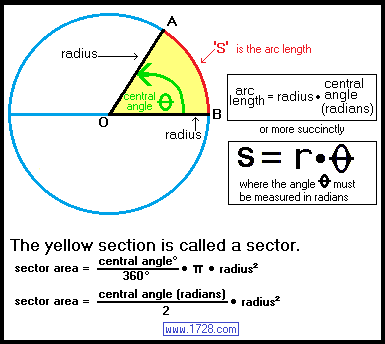
relation between arc, radius and central angle. Proof of the trigonometrical ratios of complementary angles

Arc length = [radius • central angle (radians)]

Arc length = circumference • [central angle (degrees) ÷ 360]

Proof of the trigonometric ratios of complementary allied angles

Two acute angles are complementary to each other if their sum is equal to 90°. In a right triangle the sum of the two acute angles is equal to 90°. So, the two acute angles of a right triangle are always complementary to each other.

Let ABC be a right triangle, right angled at B

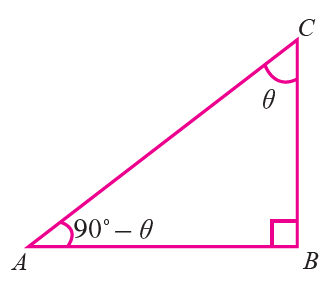
If <ACB = θ, then <BAC = 90° – θ and hence the angles <BAC and <ACB are complementary

For the angle θ, we have

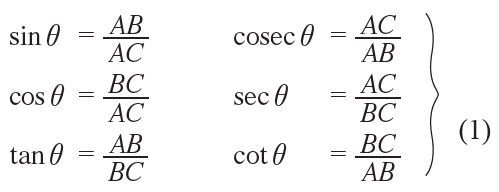
Similarly, for the angle (90° – θ), we have

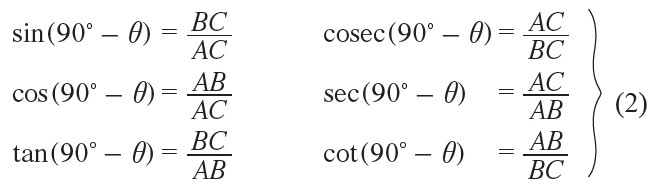
Comparing the equations in (1) and (2) we get,

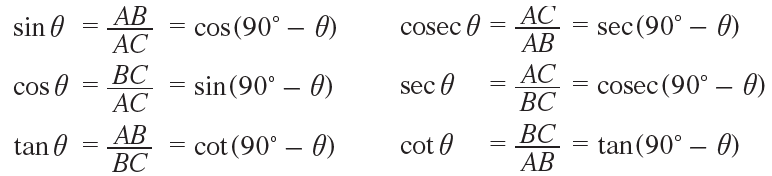
Trigonometric Ratios of Complementary Angles

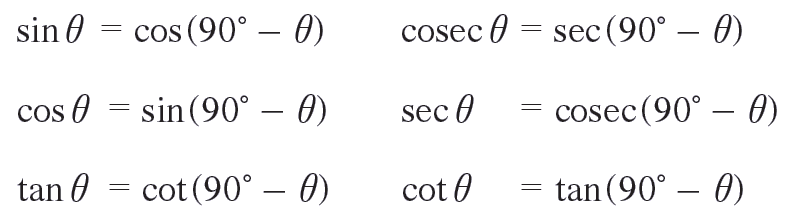
Examples: Evaluate : cos 56° / sin 34°

The angles 56° and 34° are complementary.

So, using trigonometric ratios of complementary angles, we have

cos 56° = cos (90° – 56°) = sin 34°

cos 56° / sin 34° = sin 34° / sin 34° = 1

Hence the value of cos 56° / sin 34° is 1.

In geometry, an arc is a part of the circumference of a circle or sphere. It is measured by the central angle that intercepts it. The arc length is equal to the product of the radius and the central angle, in radians.

A central angle is an angle whose vertex is at the center of a circle. The measure of a central angle is equal to the arc it intercepts, in degrees or radians.

A chord is a line segment that joins two points on a circle. The length of a chord is equal to the product of its endpoints’ distances from the center of the circle.

An inscribed angle is an angle whose vertex is on a circle and whose sides are chords of the circle. The measure of an inscribed angle is equal to half the measure of the arc it intercepts, in degrees or radians.

The tangent of an angle is equal to the ratio of the opposite side to the adjacent side. The secant of an angle is equal to the ratio of the hypotenuse to the adjacent side. The cosecant of an angle is equal to the ratio of the hypotenuse to the opposite side. The cotangent of an angle is equal to the ratio of the adjacent side to the opposite side.

Complementary angles are angles whose measures add up to 90 degrees. The trigonometric ratios of complementary angles are equal to each other. For example, the tangent of a complementary angle is equal to the cotangent of the other complementary angle.

The following is a proof of the trigonometric ratios of complementary angles:

Let $\theta$ and $\phi$ be complementary angles. Then, $\theta + \phi = 90^\circ$.

The tangent of $\theta$ is equal to the ratio of the opposite side to the adjacent side, or $\tan(\theta) = \frac{opposite}{adjacent}$.

The cotangent of $\phi$ is equal to the ratio of the adjacent side to the opposite side, or $\cot(\phi) = \frac{adjacent}{opposite}$.

Therefore, $\tan(\theta) \cot(\phi) = \frac{opposite}{adjacent} \cdot \frac{adjacent}{opposite} = 1$.

Similarly, the sine of $\theta$ is equal to the ratio of the opposite side to the hypotenuse, or $\sin(\theta) = \frac{opposite}{hypotenuse}$.

The cosine of $\phi$ is equal to the ratio of the adjacent side to the hypotenuse, or $\cos(\phi) = \frac{adjacent}{hypotenuse}$.

Therefore, $\sin(\theta) \cos(\phi) = \frac{opposite}{hypotenuse} \cdot \frac{adjacent}{hypotenuse} = 1$.

Therefore, the trigonometric ratios of complementary angles are equal to each other.

Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It is used in many fields, including engineering, surveying, and navigation.

Trigonometric ratios

The trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). They are defined as follows:

Sine = opposite side / hypotenuse
Cosine = adjacent side / hypotenuse
Tangent = opposite side / adjacent side
Cotangent = adjacent side / opposite side
Secant = hypotenuse / adjacent side
Cosecant = hypotenuse / opposite side

Trigonometric identities

Trigonometric identities are equations that are true for all values of the trigonometric variables. Some common trigonometric identities include:

Sin^2(x) + cos^2(x) = 1
tan^2(x) + 1 = sec^2(x)
cot^2(x) + 1 = cosec^2(x)

Trigonometric functions

The trigonometric functions are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). They are defined as follows:

Sine = opposite side / hypotenuse
Cosine = adjacent side / hypotenuse
Tangent = opposite side / adjacent side
Cotangent = adjacent side / opposite side
Secant = hypotenuse / adjacent side
Cosecant = hypotenuse / opposite side

The trigonometric functions can be used to solve triangles. For example, if you know the length of the hypotenuse and the length of one of the legs of a right triangle, you can use the sine function to find the length of the other leg.

The trigonometric functions can also be used to model periodic phenomena, such as the motion of a pendulum or the tides.

Trigonometric graphs

The trigonometric functions can be graphed as curves. The sine function is a wave that goes up and down, while the cosine function is a wave that goes up and down but is always above the x-axis. The tangent function is a curve that goes up and down very quickly, while the cotangent function is a curve that goes down and up very quickly. The secant function is a curve that goes up and up very quickly, while the cosecant function is a curve that goes down and down very quickly.

Trigonometric applications

Trigonometry is used in many fields, including engineering, surveying, and navigation. It is also used in music, art, and architecture.

In engineering, trigonometry is used to design bridges, buildings, and other structures. It is also used to design machines and other devices.

In surveying, trigonometry is used to measure distances and angles. It is also used to map land and to determine the location of objects.

In navigation, trigonometry is used to determine the position of ships, airplanes, and other vehicles. It is also used to determine the time.

In music, trigonometry is used to calculate the frequency of notes. It is also used to design Musical instruments.

In art, trigonometry is used to create perspective. It is also used to design buildings and other structures.

In architecture, trigonometry is used to design buildings and other structures. It is also used to design bridges and other structures.

Sure, here are some MCQs on trigonometry without mentioning the topic relation between arc, radius and central angle. Proof of the trigonometrical ratios of complementary angles:

What is the trigonometric ratio of an angle in a right triangle?
(A) The ratio of the opposite side to the hypotenuse.
(B) The ratio of the adjacent side to the hypotenuse.
(C) The ratio of the opposite side to the adjacent side.
(D) The ratio of the hypotenuse to the adjacent side.
What is the trigonometric ratio of a 30-60-90 right triangle?
(A) $\sin(30^\circ) = \frac{1}{2}$
(B) $\cos(30^\circ) = \frac{\sqrt{3}}{2}$
(C) $\tan(30^\circ) = \frac{1}{\sqrt{3}}$
(D) $\cot(30^\circ) = \sqrt{3}$
What is the trigonometric ratio of a 45-45-90 right triangle?
(A) $\sin(45^\circ) = \cos(45^\circ) = \frac{\sqrt{2}}{2}$
(B) $\tan(45^\circ) = 1$
(C) $\cot(45^\circ) = 1$
(D) $\sec(45^\circ) = \csc(45^\circ) = \sqrt{2}$
What is the trigonometric ratio of an angle in a non-right triangle?
(A) The ratio of the opposite side to the hypotenuse.
(B) The ratio of the adjacent side to the hypotenuse.
(C) The ratio of the opposite side to the adjacent side.
(D) The ratio of the hypotenuse to the adjacent side.
What is the trigonometric ratio of an angle that is not in a right triangle?
(A) It cannot be determined without knowing the length of the sides of the triangle.
(B) It can be determined by using the Pythagorean theorem.
(C) It can be determined by using the law of sines.
(D) It can be determined by using the law of cosines.
What is the trigonometric ratio of an angle that is coterminal with a 30-degree angle?
(A) $\sin(30^\circ)$
(B) $\cos(30^\circ)$
(C) $\tan(30^\circ)$
(D) $\cot(30^\circ)$
What is the trigonometric ratio of an angle that is coterminal with a 45-degree angle?
(A) $\sin(45^\circ)$
(B) $\cos(45^\circ)$
(C) $\tan(45^\circ)$
(D) $\cot(45^\circ)$
What is the trigonometric ratio of an angle that is coterminal with a 60-degree angle?
(A) $\sin(60^\circ)$
(B) $\cos(60^\circ)$
(C) $\tan(60^\circ)$
(D) $\cot(60^\circ)$
What is the trigonometric ratio of an angle that is coterminal with a 90-degree angle?
(A) $\sin(90^\circ)$
(B) $\cos(90^\circ)$
(C) $\tan(90^\circ)$
(D) $\cot(90^\circ)$
What is the trigonometric ratio of an angle that is coterminal with a 120-degree angle?
(A) $\sin(120^\circ)$
(B) $\cos(120^\circ)$
(C) $\tan(120^\circ)$
(D) $\cot(120^\circ)$

I hope these MCQs are helpful!