Probability is simply how likely something is to happen.
Whenever we’re unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics.
Tossing a Coin
When a coin is tossed, there are two possible outcomes:
heads (H) or tails (T)
We say that the probability of the coin landing H is ½ And the probability of the coin landing T is ½.
Throwing Dice
When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6.
The probability of any one of them is 16
Number of ways it can happen
Probability of an event happening = ________________________
Total number of outcomes
Data science often uses statistical inferences to predict or analyze trends from data, while statistical inferences uses probability distributions of data. Hence knowing probability and its applications are important to work effectively on data science problems.
Permutation is the different arrangements of a given number of Elements taken one by one, or some, or all at a time. For example, if we have two elements A and B, then there are two possible arrangements, AB and BA. While on the other hand Combination means selection of things. The word selection is used, when the order of things has no importance.The study of permutations and combinations is concerned with determining the number of different ways of arranging and selecting objects out of a given number of objects, without actually listing them. There are some basic counting techniques which will be useful in determining the number of different ways of arranging or selecting objects. The two basic counting principles are given below:
Fundamental principle of counting
Multiplication principle (Fundamental Principle of Counting) Suppose an event E can occur in m different ways and associated with each way of occurring of E, another event F can occur in n different ways, then the total number of occurrence of the two events in the given order is m × n .
Addition principle
If an event E can occur in m ways and another event F can occur in n ways, and suppose that both can not occur together, then E or F can occur in m + n ways.
Number of permutations of ‘n’ different things taken ‘r’ at a time is given by:-
nPr = n!/(n-r)!
The number of possible combination of r objects from a set on n objects.
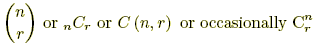
,
Permutations
A permutation is an arrangement of objects in a specific order. The number of permutations of $n$ objects is given by the formula $n!$, where $!$ is the factorial function. The factorial function is defined as follows:
$$n! = n(n-1)(n-2)\cdots 3 \cdot 2 \cdot 1$$
For example, the number of permutations of 3 objects is $3! = 3 \cdot 2 \cdot 1 = 6$.
Combinations
A combination is a selection of objects from a set without regard to order. The number of combinations of $n$ objects taken $r$ at a time is given by the formula $\binom{n}{r}$, where $\binom{n}{r}$ is the binomial coefficient. The binomial coefficient is defined as follows:
$$\binom{n}{r} = \frac{n!}{r!(n-r)!}$$
For example, the number of combinations of 3 objects taken 2 at a time is $\binom{3}{2} = \frac{3!}{2!(3-2)!} = \frac{3 \cdot 2}{2 \cdot 1} = 3$.
Factorials
The factorial function is a function that takes a positive integer as an input and returns the product of all the positive integers less than or equal to the input. The factorial function is denoted by $!$. For example, $5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$.
Binomial Theorem
The binomial theorem is a mathematical formula that expands a binomial expression into a sum of terms. The binomial expression is of the form $(a+b)^n$, where $a$ and $b$ are any real numbers and $n$ is a positive integer. The binomial theorem states that:
$$(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^k b^{n-k}$$
where $\binom{n}{k}$ is the binomial coefficient.
Probability
Probability is a measure of the likelihood that an event will occur. The probability of an event is denoted by $P(E)$. The probability of an event can be calculated using the following formula:
$$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$$
For example, if you roll a six-sided die, the probability of rolling a 6 is $\frac{1}{6}$, because there is one favorable outcome (rolling a 6) and six total possible outcomes.
Expected Value
The expected value of a random variable is the Average of the possible values of the random variable. The expected value is denoted by $E(X)$. The expected value of a random variable can be calculated using the following formula:
$$E(X) = \sum_{x \in \Omega} x P(X=x)$$
where $\Omega$ is the set of all possible values of the random variable $X$ and $P(X=x)$ is the probability that the random variable takes on the value $x$.
Standard Deviation
The standard deviation of a random variable is a measure of how spread out the possible values of the random variable are. The standard deviation is denoted by $\sigma$. The standard deviation of a random variable can be calculated using the following formula:
$$\sigma = \sqrt{\frac{\sum_{x \in \Omega} (x – E(X))^2 P(X=x)}{\sum_{x \in \Omega} P(X=x)}}$$
Normal Distribution
The normal distribution is a probability distribution that is often used to model real-world data. The normal distribution is characterized by its mean and standard deviation. The mean of the normal distribution is denoted by $\mu$ and the standard deviation of the normal distribution is denoted by $\sigma$. The normal distribution is bell-shaped, with the mean at the center of the bell. The standard deviation determines how spread out the data are. Data that are normally distributed will tend to cluster around the mean, with fewer data points further away from the mean.
Confidence Intervals
A confidence interval is a range of values that is likely to contain the true value of a Population parameter. The confidence interval is calculated using the following formula:
$$CI = \bar{x} \pm z \frac{s}{\sqrt{n}}$$
where $\
Permutations
A permutation is an arrangement of objects in a specific order. The number of permutations of n distinct objects is given by n!, where n! is the factorial of n. The factorial of a number is the product of all the positive integers less than or equal to that number. For example, 5! = 120.
Combinations
A combination is a selection of objects from a group without regard to order. The number of combinations of n distinct objects taken r at a time is given by nCr, where nCr is the binomial coefficient. The binomial coefficient is defined as n!/r!(n-r)!. For example, 5C2 = 10.
Problems Based on Probability
Probability is the likelihood of an event occurring. The probability of an event is a number between 0 and 1, inclusive. An event with a probability of 0 is impossible, and an event with a probability of 1 is certain.
The probability of two events occurring is the product of their probabilities, unless the events are dependent. Two events are dependent if the occurrence of one event affects the probability of the other event occurring.
The probability of an event occurring at least once in a series of trials is the sum of the probabilities of the event occurring in each trial.
Frequently Asked Questions
- What is the difference between a permutation and a combination?
A permutation is an arrangement of objects in a specific order, while a combination is a selection of objects from a group without regard to order.
- How do you calculate the number of permutations of n distinct objects?
The number of permutations of n distinct objects is given by n!, where n! is the factorial of n. The factorial of a number is the product of all the positive integers less than or equal to that number. For example, 5! = 120.
- How do you calculate the number of combinations of n distinct objects taken r at a time?
The number of combinations of n distinct objects taken r at a time is given by nCr, where nCr is the binomial coefficient. The binomial coefficient is defined as n!/r!(n-r)!. For example, 5C2 = 10.
- What is the probability of an event occurring?
The probability of an event occurring is a number between 0 and 1, inclusive. An event with a probability of 0 is impossible, and an event with a probability of 1 is certain.
- How do you calculate the probability of two events occurring?
The probability of two events occurring is the product of their probabilities, unless the events are dependent. Two events are dependent if the occurrence of one event affects the probability of the other event occurring.
- How do you calculate the probability of an event occurring at least once in a series of trials?
The probability of an event occurring at least once in a series of trials is the sum of the probabilities of the event occurring in each trial.
-
A bag contains 5 red balls, 3 green balls, and 2 blue balls. If one ball is drawn at random, what is the probability that it is not red?
(A) $\frac{2}{10}$
(B) $\frac{3}{10}$
(C) $\frac{5}{10}$
(D) $\frac{7}{10}$
(E) $\frac{8}{10}$ -
A coin is tossed 3 times. What is the probability of getting heads all 3 times?
(A) $\frac{1}{8}$
(B) $\frac{1}{4}$
(C) $\frac{1}{2}$
(D) $\frac{3}{4}$
(E) $\frac{7}{8}$ -
A deck of cards is shuffled and one card is drawn. What is the probability of drawing a spade?
(A) $\frac{1}{13}$
(B) $\frac{1}{4}$
(C) $\frac{1}{2}$
(D) $\frac{3}{4}$
(E) $\frac{1}{26}$ -
A box contains 10 red balls, 8 green balls, and 6 blue balls. If 3 balls are drawn at random, what is the probability that all 3 balls are red?
(A) $\frac{10}{34}$
(B) $\frac{45}{1024}$
(C) $\frac{120}{1024}$
(D) $\frac{210}{1024}$
(E) $\frac{495}{1024}$ -
A bag contains 5 red balls, 3 green balls, and 2 blue balls. If 2 balls are drawn at random without replacement, what is the probability that the first ball is red and the second ball is green?
(A) $\frac{5}{10}\cdot\frac{3}{9} = \frac{5}{36}$
(B) $\frac{5}{10}\cdot\frac{2}{9} = \frac{1}{18}$
(C) $\frac{3}{10}\cdot\frac{5}{9} = \frac{5}{36}$
(D) $\frac{3}{10}\cdot\frac{2}{9} = \frac{1}{18}$
(E) $\frac{5}{10}\cdot\frac{3}{9} + \frac{3}{10}\cdot\frac{2}{9} = \frac{10}{36} + \frac{6}{36} = \frac{16}{36} = \frac{4}{9}$ -
A coin is tossed 5 times. What is the probability of getting heads exactly 3 times?
(A) $\frac{1}{32}$
(B) $\frac{5}{32}$
(C) $\frac{10}{32}$
(D) $\frac{15}{32}$
(E) $\frac{20}{32}$ -
A box contains 10 red balls, 8 green balls, and 6 blue balls. If 2 balls are drawn at random without replacement, what is the probability that both balls are red?
(A) $\frac{10}{18}\cdot\frac{9}{17} = \frac{45}{306}$
(B) $\frac{5}{18}\cdot\frac{4}{17} = \frac{10}{252}$
(C) $\frac{5}{18}\cdot\frac{3}{17} = \frac{5}{252}$
(D) $\frac{10}{18}\cdot\frac{3}{17} = \frac{15}{252}$
(E) $\frac{5}{18}\cdot\frac{4}{17} + \frac{5}{18}\cdot\frac{3}{17} = \frac{10}{252} + \frac{5}{252} = \frac{15}{252}$ -
A bag contains 5 red balls, 3 green balls, and 2 blue balls. If 3 balls are drawn at random without replacement, what is the probability that at least one ball is red?
(A) $1 – \frac{120}{1024} = \frac{