Here is how to calculate the distance between two points when you know their coordinates:
Let us call the two points A and B
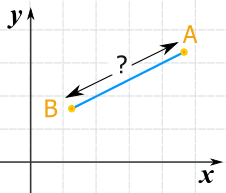
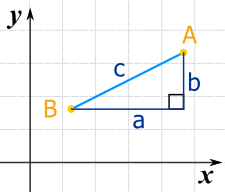
We can run lines down from A, and along from B, to make a Right Angled Triangle.
And with a little help from Pythagoras we know that: a2 + b2 = c2
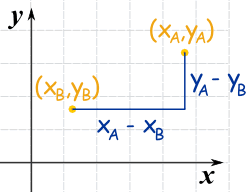
Now label the coordinates of points A and B.
xA means the x-coordinate of point A yA means the y-coordinate of point A
The horizontal distance a is (xA − xB)
The vertical distance b is (yA − yB)
Now we can solve for c (the distance between the points):
Start with: c2 = a2 + b2
Put in the calculations for a and b: c2 = (xA − xB)2 + (yA − yB)2
And the final result: c = square root of [(xA-xB)^2+(yA-yB)^2]
Examples
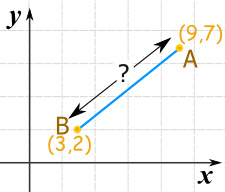
![]()
![]()
Proportional division of a line (section formula)
 ,
,
nan
Angles
-
What is an angle?
An angle is the space between two rays that share a common endpoint. -
What are the different types of angles?
There are three main types of angles: acute, right, and obtuse. An acute angle is an angle that measures less than 90 degrees. A right angle is an angle that measures exactly 90 degrees. An obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees. -
What is the sum of the angles in a triangle?
The sum of the angles in a triangle is always 180 degrees. -
What is the measure of an exterior angle of a triangle?
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles.
Parallel lines
-
What are parallel lines?
Parallel lines are lines that never intersect. -
How can you determine if two lines are parallel?
There are a few ways to determine if two lines are parallel. One way is to use the parallel postulate, which states that if two lines are cut by a transversal, then the corresponding angles are congruent. Another way to determine if two lines are parallel is to use a protractor to measure the angles between the lines. If the angles are congruent, then the lines are parallel. -
What are some properties of parallel lines?
Some properties of parallel lines include:- Parallel lines are equidistant from each other.
- The opposite sides of parallel lines are congruent.
- The alternate interior angles of parallel lines are congruent.
- The corresponding angles of parallel lines are congruent.
Perpendicular lines
-
What are perpendicular lines?
Perpendicular lines are lines that intersect at a right angle (90 degrees). -
How can you determine if two lines are perpendicular?
There are a few ways to determine if two lines are perpendicular. One way is to use the perpendicular postulate, which states that if two lines intersect at a right angle, then the opposite angles are congruent. Another way to determine if two lines are perpendicular is to use a protractor to measure the angles between the lines. If the angles are congruent, then the lines are perpendicular. -
What are some properties of perpendicular lines?
Some properties of perpendicular lines include:- The opposite angles of perpendicular lines are congruent.
- The adjacent angles of perpendicular lines are supplementary.
- The product of the slopes of perpendicular lines is -1.
Circles
-
What is a circle?
A circle is a round shape with all points the same distance from the center. -
What is the radius of a circle?
The radius of a circle is the distance from the center of the circle to any point on the circle. -
What is the diameter of a circle?
The diameter of a circle is the distance across the circle through the center. -
What is the circumference of a circle?
The circumference of a circle is the distance around the circle. -
What is the area of a circle?
The area of a circle is the amount of space enclosed by the circle.
Polygons
-
What is a polygon?
A polygon is a closed figure with straight sides. -
What are the different types of polygons?
There are many different types of polygons, but some of the most common include triangles, quadrilaterals, pentagons, hexagons, and octagons. -
What is the perimeter of a polygon?
The perimeter of a polygon is the total length of all the sides of the polygon. -
What is the area of a polygon?
The area of a polygon is the amount of space enclosed by the polygon.
Solid figures
-
What is a solid figure?
A solid figure is a three-dimensional figure. -
What are the different types of solid figures?
There are many different types of solid figures, but some of the most common include cubes, spheres, cylinders, and cones. -
What is the volume of a solid figure?
The volume of a solid figure is the amount of space enclosed by the solid figure. -
What is the surface area of a solid figure?
The surface area of a solid figure is the total area of all the faces of the solid figure.
Sure. Here are some MCQs on the topics of coordinate geometry and linear equations in two variables:
-
The coordinates of the point of intersection of the lines $y=x$ and $y=2x$ are:
(A) $(0,0)$
(B) $(1,1)$
(C) $(2,2)$
(D) $(3,3)$ -
The equation of the line that passes through the points $(-2,3)$ and $(4,5)$ is:
(A) $y=2x+1$
(B) $y=-2x+1$
(C) $y=x+2$
(D) $y=-x+2$ -
The slope of the line that passes through the points $(-2,3)$ and $(4,5)$ is:
(A) $\frac{5}{2}$
(B) $\frac{2}{5}$
(C) $-\frac{5}{2}$
(D) $-\frac{2}{5}$ -
The equation of the line that is perpendicular to the line $y=2x+1$ and passes through the point $(-2,3)$ is:
(A) $y=-\frac{1}{2}x-2$
(B) $y=\frac{1}{2}x-2$
(C) $y=2x-2$
(D) $y=-2x-2$ -
The distance between the points $(-2,3)$ and $(4,5)$ is:
(A) $\sqrt{13}$
(B) $\sqrt{25}$
(C) $\sqrt{34}$
(D) $\sqrt{49}$ -
The midpoint of the line segment joining the points $(-2,3)$ and $(4,5)$ is:
(A) $(-1,4)$
(B) $(1,4)$
(C) $(2,4)$
(D) $(3,4)$ -
The area of the triangle with vertices $(-2,3)$, $(4,5)$, and $(0,0)$ is:
(A) $\frac{1}{2}$
(B) 1
(C) 2
(D) 3 -
The equation of the circle with center $(-2,3)$ and radius 5 is:
(A) $(x+2)^2+(y-3)^2=25$
(B) $(x-2)^2+(y-3)^2=25$
(C) $(x+2)^2+(y+3)^2=25$
(D) $(x-2)^2+(y+3)^2=25$ -
The equation of the parabola with vertex $(-2,3)$ and focus $(-2,1)$ is:
(A) $y=2x^2+5x+4$
(B) $y=2x^2-5x+4$
(C) $y=-2x^2+5x+4$
(D) $y=-2x^2-5x+4$ -
The equation of the ellipse with center $(-2,3)$, major radius 5, and minor radius 3 is:
(A) $\frac{(x+2)^2}{25}+\frac{(y-3)^2}{9}=1$
(B) $\frac{(x-2)^2}{25}+\frac{(y-3)^2}{9}=1$
(C) $\frac{(x+2)^2}{9}+\frac{(y-3)^2}{25}=1$
(D) $\frac{(x-2)^2}{9}+\frac{(y+3)^2}{25}=1$
I hope these questions are helpful!