Determination of focal length of concave miror by single pin method. [Relation between u-v-f (numerical examples)
Spherical mirrors
It is a mirror which has the shape of a piece cut out of a spherical surface. Two types of spherical mirrors are;
Concave mirror: Its inner concave surface reflects, and has polished outer surface. Convex mirror: Its outer convex surface reflects, and has polished inner surface.
Pole (P): The centre of the spherical mirror.
Centre of curvature (C): The centre of the sphere, of which the mirror is a part.
Principal focus (F): The point on the principal axis, on which all parallel rays meet after reflection.
Radius of curvature (R): The distance between pole and centre of curvature.
Focal length (f): The distance between pole and principal focus
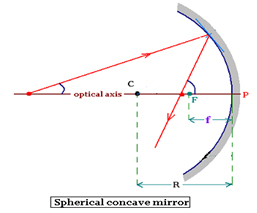
Concave Mirror
Concave mirrors have the reflecting surface that bulges inward. They are also called converging mirrors because it converges all parallel beam of Light incident on it. Unlike a flat mirror, concave mirrors can form real images that are projected out in front of the mirror at the place where the light focuses. Concave mirrors can be used in satellite dishes, vehicle headlights, astronomical telescopes and many more areas.
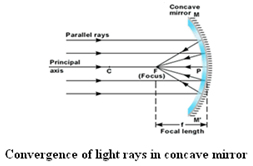
Mirror Formula The equation connecting the distance between mirror and object (u), distance between mirror and image (v), and the focal length of the mirror (f) is called mirror formula.
![]()
Or ; The focal length of the concave mirror,
![]()
Focal length by graphical method
From u-v graph
We can measure the focal length of the given concave mirror graphically by plotting graph between u and v. For this, plot a graph with u along X axis and v along Y axis by taking same scale for drawing the X and Y axes. A curve is obtained. The point at which the bisector meets the curve gives the radius of curvature (R).
Now focal length can be calculated from the relation, R = 2f.
From 1/u – 1/v graph : We can also measure the focal length by plotting graph between 1/-u and 1/v. Plot a graph with 1/u along X axis and 1/v along Y axis by taking same scale for drawing the X and Y axes. The graph is a straight line intercepting the axes at A and B. The focal length can be calculated by using the relations, OA=OB= 1/f.,
Determination of focal length of concave mirror by single pin method
The focal length of a concave mirror is the distance from the mirror to the point where all light rays parallel to the principal axis converge after being reflected by the mirror. The focal length can be determined by using the single pin method.
To determine the focal length of a concave mirror using the single pin method, you will need the following materials:
- A concave mirror
- A pin
- A ruler
- A screen
Procedure:
- Fix the concave mirror on a stand.
- Place the pin on the principal axis of the mirror, in front of the mirror.
- Adjust the position of the pin until its image is formed on a screen placed behind the mirror.
- Measure the distance between the pin and the mirror (u).
- Measure the distance between the image of the pin and the mirror (v).
- Use the following formula to calculate the focal length of the mirror:
$$f = \frac{uv}{u-v}$$
Relation between u-v-f:
The distance between the object (u) and the mirror, the distance between the image (v) and the mirror, and the focal length of the mirror (f) are related by the following formula:
$$f = \frac{uv}{u-v}$$
Numerical examples:
Suppose that u = 10 cm and v = 20 cm. Then, the focal length of the mirror is:
$$f = \frac{uv}{u-v} = \frac{(10 \text{ cm})(20 \text{ cm})}{(10 \text{ cm}) – (20 \text{ cm})} = 15 \text{ cm}$$
Applications of concave mirrors
Concave mirrors are used in a variety of applications, including:
- Telescopes: Concave mirrors are used in telescopes to collect light from distant objects and focus it on a small area. This allows astronomers to see objects that are too faint to be seen with the naked eye.
- Microscopes: Concave mirrors are used in microscopes to collect light from a small object and focus it on a larger area. This allows scientists to see objects that are too small to be seen with the naked eye.
- Projectors: Concave mirrors are used in projectors to focus light from a lamp onto a screen. This allows images to be projected onto a large screen.
- Flashlights: Concave mirrors are used in flashlights to focus light from a bulb into a narrow beam. This allows the flashlight to illuminate objects that are far away.
- Solar cookers: Concave mirrors are used in solar cookers to focus sunlight onto a small area. This allows the solar cooker to cook food without using any fuel.
Conclusion
Concave mirrors are a type of mirror that curves inward at the center. They have a variety of applications, including telescopes, microscopes, projectors, flashlights, and solar cookers. The focal length of a concave mirror can be determined by using the single pin method.
Determination of focal length of concave mirror by single pin method
The focal length of a concave mirror can be determined by the single pin method. This method involves placing a pin at a distance greater than the focal length of the mirror and then observing the image of the pin formed by the mirror. The image of the pin will be real, inverted, and magnified. The focal length of the mirror can be calculated by measuring the distance between the mirror and the image of the pin.
Relation between u-v-f [numerical examples]
The following equations relate the object distance (u), image distance (v), and focal length (f) of a concave mirror:
1/f = 1/u + 1/v
f = uv/u + v
where u is the object distance, v is the image distance, and f is the focal length.
For example, if the object distance is 10 cm and the image distance is 20 cm, then the focal length of the mirror is:
f = uv/u + v = 10 * 20 / 10 + 20 = 14.28 cm
If the object distance is 20 cm and the image distance is 10 cm, then the focal length of the mirror is:
f = uv/u + v = 20 * 10 / 20 + 10 = 11.11 cm
-
A concave mirror forms an image of an object placed 10 cm in front of it at a distance of 20 cm from the mirror. What is the focal length of the mirror?
(A) 10 cm
(B) 20 cm
(C) 30 cm
(D) 40 cm -
A convex mirror forms an image of an object placed 10 cm in front of it at a distance of 20 cm from the mirror. What is the focal length of the mirror?
(A) 10 cm
(B) 20 cm
(C) 30 cm
(D) 40 cm -
A ray of light strikes a concave mirror at an angle of incidence of 30 degrees. The angle of reflection is
(A) 30 degrees
(B) 45 degrees
(C) 60 degrees
(D) 90 degrees -
A ray of light strikes a convex mirror at an angle of incidence of 30 degrees. The angle of reflection is
(A) 30 degrees
(B) 45 degrees
(C) 60 degrees
(D) 90 degrees -
A concave mirror forms a real image of an object that is 20 cm tall. The image is 10 cm tall. What is the magnification of the image?
(A) 1
(B) 2
(C) 3
(D) 4 -
A convex mirror forms a virtual image of an object that is 20 cm tall. The image is 10 cm tall. What is the magnification of the image?
(A) 1
(B) 2
(C) 3
(D) 4 -
A concave mirror forms a real image that is inverted. The object is placed 10 cm in front of the mirror. The focal length of the mirror is 20 cm. What is the magnification of the image?
(A) 1
(B) 2
(C) 3
(D) 4 -
A convex mirror forms a virtual image that is erect. The object is placed 10 cm in front of the mirror. The focal length of the mirror is 20 cm. What is the magnification of the image?
(A) 1
(B) 2
(C) 3
(D) 4 -
A concave mirror forms a real image that is magnified. The object is placed 10 cm in front of the mirror. The focal length of the mirror is 20 cm. What is the distance between the object and the image?
(A) 10 cm
(B) 20 cm
(C) 30 cm
(D) 40 cm -
A convex mirror forms a virtual image that is diminished. The object is placed 10 cm in front of the mirror. The focal length of the mirror is 20 cm. What is the distance between the object and the image?
(A) 10 cm
(B) 20 cm
(C) 30 cm
(D) 40 cm